MATLAB可視化圖形(搭配Google搜尋器Calculator渲染引擎)


可視化圖形對我們非常重要，透過視覺上的輔助可以幫助我們解決更多問題，比方說尋找一個函數的最高、最低點等等，而MATLAB也提供非常強大的繪圖功能，非常直得我們去使用。


最近發現了Google搜尋引擎支援3D繪圖操作，使用的是WebGL技術，覺得非常地新奇、有趣。相關官方文件參考如下:
Manage calculator, unit converter & color codes

Google Calculator 圖形可視化使用方式

其搜尋規則非常簡單，先看一個例子:
5 + (-sqrt(1 - x² - (y - abs(x))²)) * cos(30 * ((1 - x² - (y - abs(x))²))), x is from -1 to 1, y is from -1 to 1.5, z is from 1 to 6
我們只須要首先將上述公式，隨後搭配參數範圍(可選)，查詢欄位第一個位置基本就會幫你做可視化動作。上述Query的輸出樣貌如下:


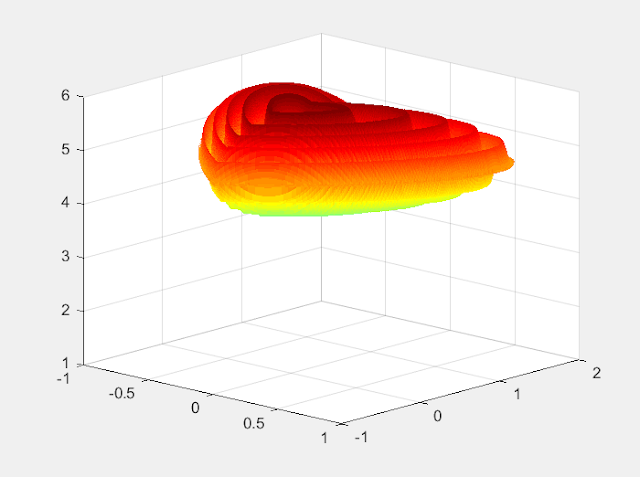
我們可以看到，其輸出為一個有連續皺褶的愛心形狀，除了中間圖形可以透過滑鼠轉換角度與縮放之外，右下角可以讓我們重新自定義function的顯示範圍。
預設圖形若是3D圖形，是會旋轉的，這個功能我們可以透過播放(Play)與暫停(Pause)按鈕進行控制。圖示如下:


此外，如果畫面被自己調亂或者須要重設，我們還可以透過左上角的"Back to the original zoom, rotation and scale"按鈕進行重置。圖示如下:

而提到zoom縮放，他也提供兩種縮放方式，包括相機(Camera)模式與函數(Function)模式。

在相機(Camera)模式下，你可以想成現在的主角是在瀏覽google頁面的你，所以當前所做的縮放是對整個可視化圖形、Function進行縮放。
放大效果如下:

縮小效果如下:

而在函數(Function)模式下，則是把Function的世界進行固定，所以當前所做的縮放會是單純對圖形進行縮放，對圖形來說Function的邊界即是極限，若超出則會被裁切掉。
放大效果如下:

縮小效果如下:

以上兩種縮放方式，你也可以觀察右下角的邊界極值的變化看出其進行顯示的方式。
當然，若一開始你並不想指定各軸的顯示範圍，這也是沒關係的，預設會將讓圖形的輸出盡量貼近整個視窗。比方說:
5 + (-sqrt(1 - x² - (y - abs(x))²)) * cos(30 * ((1 - x² - (y - abs(x))²)))
輸出效果如下:


MATLAB繪圖

大致介紹完這項好用的繪圖工具後，我們將來試著自己也實現如何使用MATLAB語言進行函數可視化，生活中處處可見的東西，都能成為我們學習的題材，哪怕在簡單的任務，若能從中找尋更細膩的細節，進一步去強化自己，更能夠去獲得成就與興趣。
為了呼叫的方便，我們這裡選擇將每一個函數用MATLAB函式進行包裝，避免造成主程式中有雜亂與混淆現象。
首先，我們先來試著實作一開始提及的愛心形狀函數，建立一個"love_fun.m"檔案:
function [output] = love_fun(x, y)
    output = 5 + (-sqrt(1 - x.^2 - (y - abs(x)).^2)) .* cos(30 * (1 - x.^2 - (y - abs(x)).^2));
end
我們將輸入x, y兩個輸入參數，而output代表函數輸出，且為了呼應MATLAB的主要應用，也就是矩陣運算，這些參數我們首先定義為矩陣形式。注意到我們的運算式中，有使用到了dot(.)來進行元素的相乘，而不是一般的矩陣乘法，這是因為原本函數是設計給x, y皆為單一數字時的情況，當我們轉換為矩陣的形式作為輸入時，我們也得保持原先的元素位置進行相乘，如此兩者輸出數值才會等價。除此之外，其他表現形式並無太大相異之處。
註: 元素的相乘便是所謂的Element-wise product，又可以稱為Hadamard product，是一種矩陣的特殊相乘方式。在MATLAB中，若在運算符(如*、^、/等等)之前放置dot(.)符號，便可以將運算變成Element-wise的操作。
兩種不同的矩陣乘法運算如下圖所示:

我們先解說一下繪圖步驟，一般而言，繪圖首先會須要給定目標座標，也就是所有須要被用來建構圖形的點，而在MATLAB提供了幾個方便我們輸出圖形的函式，可以用來表示我們的目標函數，分別為plot()、plot3()、surf()、contour()以及meshc()。
基本上這些函式繪圖時，會依據給定的順序(若為matrix，以column優先)進行描繪，而他們之間的差異與應用目的如下:
  1. plot(): 主要用來畫線，也能畫點(當點因為輸入參數順序被判斷獨立於其他點，而不與其他點相連時會發生)，以二維空間表示。兩軸座標輸入參數的型態可以為scalar、vector與matix。
  2. plot3(): 也是透過描出線形的方式，能畫點(當點因為輸入參數順序被判斷獨立於其他點，而不與其他點相連時會發生)，但以三維空間表示。三軸座標輸入參數的型態可以為scalar、vector or matix。
  3. surf(): 以建構一個面為前提，會將各點與相鄰的點進行相連，所以可以控制的屬性也與面以及連接線相關。這邊要注意到，若將三軸座標輸入參數以x、y、z表示，x與y可以為vector or matix，但z必須為matix。
  4. contour(): 用來描繪一個圖形的輪廓，可以想成將圖形投影到x、y軸後(形成一個面)，以顏色等資訊來表示高度(z軸)。簡而言之的話，等高線圖便是其中的一個例子。若將三軸座標輸入參數以x、y、z表示，x與y可以為vector or matix，但z必須為matix。
  5. meshc(): 結合surf()以及contour()各自所輸出的繪圖資訊並一同進行顯示，contour plot將會依附在surface plot底下，若將三軸座標輸入參數以x、y、z表示，x與y可以為vector or matix，但z必須為matix。
所以你可以知道，以要顯示的空間維度劃分的話:
  1. 要表示二維空間圖形，可以使用plot()。
  2. 若是要表示三維空間圖形，則可以使用plot3()、surf()、contour()、meshc()。
以輸入參數型態劃分: 這牽涉到其繪圖的過程，也是可以分兩種。
  1. 因為以描線為主要顯示手段，點座標資訊輸入參數可以為scalar、vector與matix，如plot()以及plot3()。
  2. 以形成一個面為主要顯示手段，由於矩陣的在MATLAB的表現形式限制，若將三軸座標輸入參數以x、y、z表示，x與y可以為vector or matix，但z必須為matix。如surf()、contour()以及meshc()。

註: 基本上像是plot()與plot3()等函式中有"Maker"屬性，代表的是要不要在視窗上以視覺符號或用哪些符號來顯示點，而預設"Maker"屬性為"none"，這意味著點在圖上是透明的，所以若因為點發生重疊等情況，導致不與其他點被相連起來，視覺上可能會找不到點在哪，但其實可透過以知座標與滑鼠(或是"Brush/Select Data"功能)在繪圖視窗上找尋到其蹤跡，當然，若不希望這種情況發生，其實只要修改"Maker"屬性就行。
再來就是我們的主程式的部分，我們先建立一個"main.m"檔案。
由於我們想要模擬剛才介紹到的愛心圖形，所以我們本次使用plot3()以及surf()函式來描繪圖形。正好可以讓我們來看看這兩種的表現有何不同。
首先是plot3():
N = 100;
x = linspace(-1, 1, N);
y = linspace(-1, 1.5, N);
[x2, y2] = meshgrid(x, y);
z = love_fun(x2, y2);
plot3(x2, y2, real(z), 'Marker', 'o', 'MarkerSize', 1.0, 'MarkerEdgeColor', 'red','Color', [0.9 0.6 0.1]);
我們為了方便控制點的數量，宣告了N變數來表示點的數量。而linspace函式可以幫助我們在一段範圍之間生成固定點數量的點資訊，且這些點之間的間隔是被平均分配且固定的，輸出為vector。
而meshgrid顧名思義，可以幫助我們產生網狀的格子分佈，輸出為matrix。用法為輸入兩個vector分別代表x、y兩軸，將會輸出二維的x'以及y'，輸出的大小自然由x及y的長度決定，其所擴充的維度方式如下圖所示:


而我們得到的x'以及y'，正好符合我們當初定義好的函式輸入參數的型態，我們只須要呼叫love_fun()便能得到目標函數的輸出。
這邊要特別注意到，此函數的輸出，在某些部分會產生虛數，為了正常將圖形輸出出來，我們只提取實數部位，只用到了real()這個函式。
再來就是呼叫plot3()進行繪圖了，我們先將點以空心圓圈表示，其大小也縮小六倍(原預設值為6點，一點為1/72英寸)，點邊框顏色指定為紅色。為了更明顯地區別點以及連接線，將連接線的顏色用相似色系的顏色表示，只用RGB格式指定。
輸出如下所示:


我們可以看到由於捨棄虛數虛部的關係，導致在z軸刻度5的位置有一個平面，這個是我們不期望的，所以接下來我們將使用其他繪圖函式進行修改。
我們將繪圖函式改為surf():
surf(x2, y2, real(z));
輸出效果如下:


我們可以看到其所繪製的圖形更接近Google Calculator的3D圖形輸出了。但我們還沒解決在z軸刻度5的位置的平面的問題。我們先擱著，先來介紹一個修改圖形顏色的方式。我們可以使用colormap()進行圖形顏色的改變(適用於surf()、contour()以及meshc()圖形的輸出)。
colormap()的輸入有很多種方式，如MATLAB內建的colormap function與顏色字串(像是'red'、'r'、'blue'、'b'等等)，以及RGB vector(像是[1 0 0]、[0 0 1]等等)。這邊我們為了貼近一開始看到的愛心圖顏色，我們可以繼續輸入以下指令:
c = jet;
% 這個操作會修改到jet的矩陣，直到figure視窗被關閉才會重置(clear等指令無效)
c2 = c(33:64, :);
colormap(c2)
其中，jet便是MATLAB內建的colormap function，呼叫它會回傳64 * 3的矩陣，是一連串的RGB vector組成，顏色由藍至紅，如下所示:


而我們的目標抓個大概，只須要後半部分，也就是偏綠色至紅色的部位，所以我們另外定義一個c2去接收新的矩陣。最後透過colormap()進行指定。
輸出效果如下:


而一開始Google Calculator的3D圖形的輸出，z軸的範圍是1至6，這我們也可以透過zlim()來指定(若要修改x、y軸的可視範圍，則分別可以使用xlim()、ylim())。我們繼續輸入以下指令:
zlim([1 6])
現在的輸出為:


我們終於要來把在z軸刻度5位置的平面給移除了，這邊我們得要修改一下surface的屬性，大致的概念就是把指定z軸數值範圍，並讓其變為透明，我們不去直接移除不必要的元素，是為了避免圖形線條與形狀跑掉。
我們修改並新增以下程式碼:
s = surf(x2, y2, real(z));
s.AlphaData = (real(z) ~= 5);
s.FaceColor = 'texturemap';
s.FaceAlpha = 'texturemap';
我們為了改變某區域的透明度，須要先將'FaceAlpha'屬性修改為'texturemap'，連帶的，'FaceAlpha'屬性也須修改為'texturemap'。
再來就是指定哪些區域須要變透明，透過'AlphaData'來指定，其大小與z軸輸入參數大小一樣，元素大小由0至1，越小代表越透明。
輸出效果如下:


我們可以看到網格，也就是連接線依然存在，這個我們可以透過兩種方式來解決，第一種為將surface的'EdgeColor'屬性修改為'none'，表示不需要連接線，第二種為利用shading這個關鍵字來修改color shading，這可以讓整體圖形顏色盡量一致。
輸入以下程式碼:
s.EdgeColor = 'none';
% or
shading interp
% or
shading flat
大致效果如下:


我們可以看到圖形是有些粗糙的，我們可以透過增加點數量來改善。
修改為以下程式碼:
N = 500;
這個變數讓我們可以方便去修改點的數量，雖然非必要，但也起到非常重要的效果。
現在的效果如下:


最後附上俯視圖以及放大圖:



至此，一個漂亮的愛心便透過MATLAB程式輸出出來了。
本次我們介紹了如何使用MATLAB的部分可視化功能，並且將生活中可能遇到的工具功能進行實現，不僅讓我們更了解這些工具可能的運作步驟，也更了解MATLAB，最重要的，這使我們能夠更進一步成長。當然，它還有很多相關功能與技巧可以去使用，我們將繼續在往後的篇章進行介紹。

作者： 於
     
標籤： , , , , , , , ,

沒有留言:

張貼留言

訂閱： 張貼留言 (Atom)